We have already studied how to find equations of tangent lines to functions and the rate of change of a function at a specific point. In all these cases we had the explicit equation for the function and differentiated these functions explicitly. Suppose instead that we want to determine the equation of a tangent line to an arbitrary curve or the rate of change of an arbitrary curve at a point. In this section, we solve these problems by finding the derivatives of functions that define y[/latex] implicitly in terms of x[/latex].
In this section, we solve these problems by finding the derivatives of functions that define implicitly in terms of . If we want to find the slope of the line tangent to the graph of at the point , we could evaluate the derivative of the function at . On the other hand, if we want the slope of the tangent line at the point , we could use the derivative of . However, it is not always easy to solve for a function defined implicitly by an equation. Fortunately, the technique of implicit differentiation allows us to find the derivative of an implicitly defined function without ever solving for the function explicitly.
The process of finding using implicit differentiation is described in the following problem-solving strategy. Derivatives can be generalized to functions of several real variables. In this generalization, the derivative is reinterpreted as a linear transformation whose graph is the best linear approximation to the graph of the original function. The Jacobian matrix is the matrix that represents this linear transformation with respect to the basis given by the choice of independent and dependent variables.
It can be calculated in terms of the partial derivatives with respect to the independent variables. For a real-valued function of several variables, the Jacobian matrix reduces to the gradient vector. The vertical tangent to a curve occurs at a point where the slope is undefined . This can also be explained in terms of calculus when the derivative at a point is undefined.
There are many ways to find these problematic points ranging from simple graph observation to advanced calculus and beyond, spanning multiple coordinate systems. The method used depends on the skill level and the mathematic application. The first step to any method is to analyze the given information and find any values that may cause an undefined slope. It cannot be a function on the tangent bundle because the tangent bundle only has room for the base space and the directional derivatives.
Because jets capture higher-order information, they take as arguments additional coordinates representing higher-order changes in direction. The space determined by these additional coordinates is called the jet bundle. The derivative of a function has many applications to problems in calculus. The derivative of a function at a point is the slope of the tangent line at this point. The normal line is defined as the line that is perpendicular to the tangent line at the point of tangency.
Because the slopes of perpendicular lines are negative reciprocals of one another, the slope of the normal line to the graph of f is −1/ f′. Using implicit differentiation find y', so that you have a formula for slopes of tangent lines to the graph of the original function. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point.
The tangent line is the best linear approximation of the function near that input value. Example let find those points on the graph at which the tangent line is a horizontal. To find a horizontal tangent, you must find a point at which the slope of a curve is zero, which takes about 10 minutes when using a calculator. This calculus video tutorial shows you how to find and write the equation of the horizontal tangent line and normal line and point slope form and slope inter. Now that we have seen the technique of implicit differentiation, we can apply it to the problem of finding equations of tangent lines to curves described by equations.
A vertical tangent is parallel to y-axis and hence its slope is undefined. After getting the points, we can find the equation of the vertical tangent line using the point-slope form. A horizontal tangent is parallel to x-axis and hence its slope is zero. We know that the slope is nothing but the derivative of the function. So to find the points where there are horizontal tangents just set the derivative of the function to zero and solve. After getting the points, we can find the equation of the horizontal tangent line using the point-slope form.
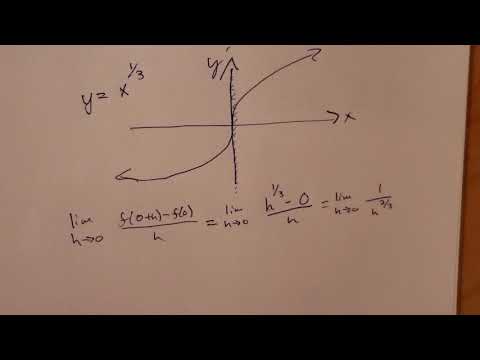
This result is the equation of the tangent line to the given function at the given point. When we have a function that isn't defined explicitly for ??? The derivative of a function can, in principle, be computed from the definition by considering the difference quotient, and computing its limit.
You can use your calculator to solve the equation that must be true for a vertical tangent line." Note that where functions have vertical tangent lines, they are not differentiable at that point. Implicit differentiation calculator is an online tool through which you can calculate any derivative function in terms of x and y. The implicit derivative calculator with steps makes it easy for biggeners to learn this quickly by doing calculations on run time. The step by step results of implicit derivative calculator makes you complete a specific task within minuets. Find the equations of all horizontal and vertical tangent lines.
Round to three decimals. So what I need to do first is get why by itself. And for this one I'm going to subtract the X squared first, interesting And then I'm gonna divide both sides by 12.
So in my calculator I'm going to put y equals negative x squared over 12. Then for this uh tangent line I'm going to subtract X and add three. So from here I'm gonna put both of these into my calculator. Both of these functions. Mhm negative X squared over 12 and then a negative X.
And then I'm gonna head graph if you wish you do and you should see them intersecting each other at one point. Now to determine that point, I'm gonna hit second trees and then intersect which is number five. And then get really close to that tangent point And hit enter three times.
And that tells me that my point of tangent C. The process of finding a derivative is called differentiation. The reverse process is called antidifferentiation. The fundamental theorem of calculus relates antidifferentiation with integration. Differentiation and integration constitute the two fundamental operations in single-variable calculus. We use implicit differentiation to find derivatives of implicitly defined functions .
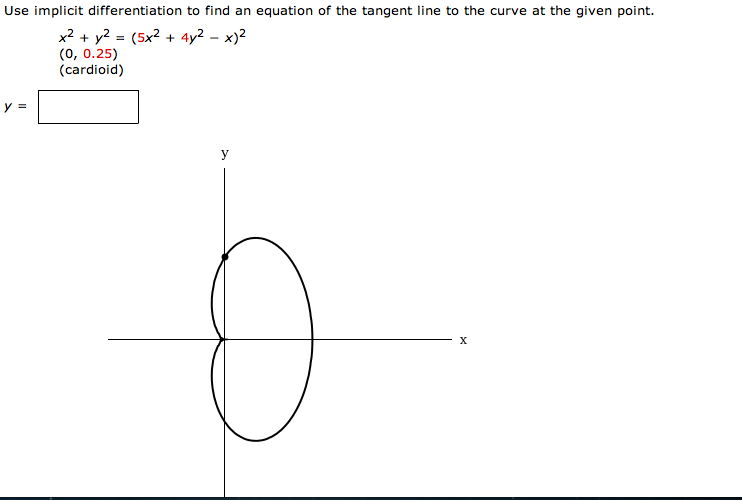
Calculus is a reformulation of the study of elementary mathematics, facilitated through the use of limits. This process uses the formulas and techniques from pre-calculus courses, and produces a more powerful and widely applicable use of concepts. This course meets all Advanced Placement Program requirements and prepares students to take the AP exam for college credit and/or placement. Topics include limits and their properties, differentiation, applications of differentiation, integration, applications of integration, and techniques of integration. Implicit differentiation allows us to find slopes of tangents to curves that are clearly not functions . We are using the idea that portions of y[/latex] are functions that satisfy the given equation, but that y[/latex] is not actually a function of x[/latex].
In addition to finding the area under a parametric curve, we sometimes need to find the arc length of a parametric curve. In the case of a line segment, arc length is the same as the distance between the endpoints. If a particle travels from point A to point B along a curve, then the distance that particle travels is the arc length. To develop a formula for arc length, we start with an approximation by line segments as shown in the following graph. Calculus, known in its early history as infinitesimal calculus, is a mathematical discipline focused on limits, functions, derivatives, integrals, and infinite series.
Isaac Newton and Gottfried Leibniz independently discovered calculus in the mid-17th century. However, each inventor claimed the other stole his work in a bitter dispute that continued until the end of their lives. This notation is used exclusively for derivatives with respect to time or arc length. It is typically used in differential equations in physics and differential geometry. The dot notation, however, becomes unmanageable for high-order derivatives and cannot deal with multiple independent variables. The tangent line of a curve at a given point is a line that just touches the curve at that point.
The tangent line in calculus may touch the curve at any other point and it also may cross the graph at some other point as well. In that case, the line is called a secant line. Here, we can see some examples of tangent lines and secant lines. Let us see how to find the slope and equation of the tangent line along with a few solved examples. Also, let us see the steps to find the equation of the tangent line of a parametric curve and a polar curve.
The derivative has many applications in "real life"; one of the most useful is to find the rate of change of one variable with respect to another. Think of a rate of change, or sometimes called an instantaneous rate of change as how fast something is changing at a certain point, like a point in time. We hope you liked our implicit function calculator. There are other useful online tools on this website which you can use such as third derivative calculator or chain rule calculator with steps.
Tools like these can save your time which you spend doing manual calculations. Besides this implicit differential calculator, you can also use tangent line approximation calculator for finding derivative of a slope or curve. By using implicit differentiation, we can find the equation of a tangent line to the graph of a curve.
Determine the \(x\)-\(y\) coordinates of the points where the following parametric equations will have horizontal or vertical tangents. Test the point by plugging it into the formula . If the right-hand side of the equation differs from the left-hand side , then there is a vertical tangent line at that point. We'll use implicit differentiation, since solving our equation for ??? Is a little tedious and gives us an ugly value. Remember that whenever we take the derivative of a term involving ???
A tangent of a curve is a line that touches the curve at one point. It has the same slope as the curve at that point. A vertical tangent touches the curve at a point where the gradient of the curve is infinite and undefined. On a graph, it runs parallel to the y-axis.
Explain how a derivative uses limits to find slopes of tangent lines. ¶Before we embark on setting the groundwork for the derivative of a function, let's review some terminology and concepts. Remember that the slope of a line is defined as the quotient of the difference in y-values and the difference in x-values.
Implicit Differentiation. Objectives Students will be able to Calculate derivative of function defined implicitly. Determine the slope of the tangent.
Because the limit of a function tends to zero if and only if the limit of the absolute value of the function tends to zero. This last formula can be adapted to the many-variable situation by replacing the absolute values with norms. Most functions that occur in practice have derivatives at all points or at almost every point. Early in the history of calculus, many mathematicians assumed that a continuous function was differentiable at most points. Under mild conditions, for example if the function is a monotone function or a Lipschitz function, this is true. However, in 1872 Weierstrass found the first example of a function that is continuous everywhere but differentiable nowhere.
This example is now known as the Weierstrass function. In 1931, Stefan Banach proved that the set of functions that have a derivative at some point is a meager set in the space of all continuous functions. Informally, this means that hardly any random continuous functions have a derivative at even one point. Consequently, the secant lines do not approach any single slope, so the limit of the difference quotient does not exist. Note that we may have to use implicit differentiation to find the derivative f ' if the function is implicitly defined.
How To Find Horizontal Tangent Line Implicit Differentiation We are using the idea that portions of are functions that satisfy the given equation, but that is not actually a function of . Use implicit differentiation to determine the equation of a tangent line. The next topic that we need to discuss in this section is that of horizontal and vertical tangents. We can easily identify where these will occur (or at least the \(t\)'s that will give them) by looking at the derivative formula. Rather than ignoring the relationship between the two points, as in the first form, this formula relies upon it. The symbol y2 is now f(x + h), and y1 is f.
The major difference here, though, is that x2 has been replaced by the first x plus some change "h". The slope formula's premise still stands, however, as the new form does in fact calculate change in y over change in x. What we want is a line tangent to the function at (1, 1/2) -- one that has a slope equal to that of the function at (1, 1/2).
We have been using slopes of secant lines over tiny intervals to approximate derivatives. In this example, we'll turn that around – we'll use the derivative to approximate the slope of the secant line. In the next few sections, we'll get the derivative rules that will let us find formulas for derivatives when our function comes to us as a formula.

















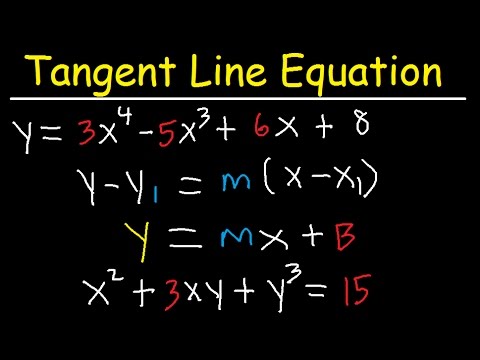



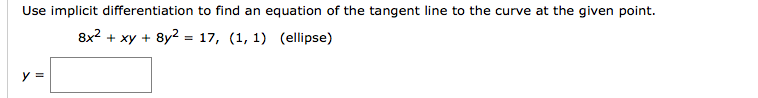



No comments:
Post a Comment
Note: Only a member of this blog may post a comment.